细嚼慢咽布隆过滤器(Bloom Filter)

Posted on | In

在海量数据处理的场景之下，Bloom Filter 是一种空间效率很高的数据结构，它是一个可以快速判断元素是否存在的概率算法，但是前提是在一定的容错率之下，本文特此进行了一番介绍。

搜索微信公众号【 Jet与编程 】体验更多有趣功能和文章哦。

背景

在上篇【链接】中，我们借助 Java 的 BitSet 源码尝试着理解了下 BitMap 算法，但是有一个很致命的劣势没有解决，那就是很尴尬的数据碰撞问题。
啥意思呢，再次解释一下下，BitMap 中我们只是很简单地初始化了一个 Long 数组，然后使用一个个小小的 bit 位来表示一个数据的存在与否，但是其中必然会面对哈希碰撞问题。
我们画张简图来回顾下 BitMap 算法。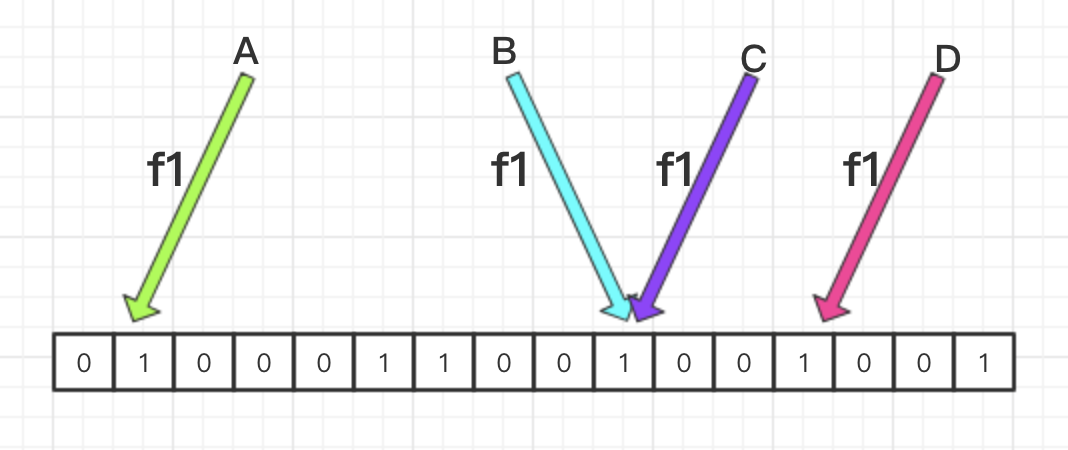
BitMap 算法简介
如上图所示，hash function 均为 f1，数据 A 和 D 指向的位是1，所以肯定是存在的，而 B 和 C 指向的都是同一个位，所以哈希碰撞就是这样很容易地产生了。
即：位上无元素则表示该数据肯定不存在，位上有元素则只能表示该数据可能存在。

BF 算法简介

有弊端总有解决之道，此处正好引入本文主要介绍的一种算法：布隆过滤器，英文名为 Bloom Filter，下文简称 BF 算法。
同样，我们还是先画一张简图来直观地认识下 BF 算法。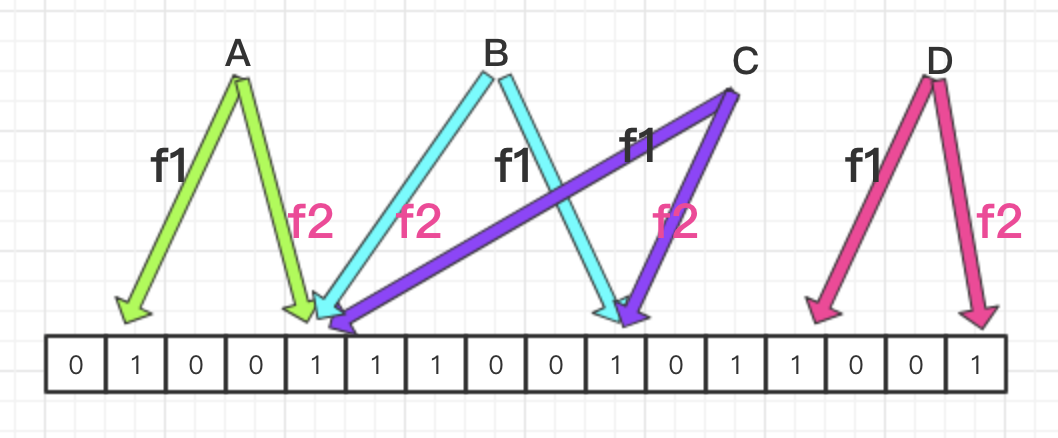
Bloom Filter 算法简介

由上图我们可以看出，此时的 A、B、C、D 四个数据各自经过 f1 和 f2 方法进行两次 hash 算法，然后分别指向位上面，只有当 f1 和 f2 指向的位上面都为 1 时，才会标记为存在。

  1. 举例 1：上图的 A 和 B，虽然 f2 计算的位都是同样的 1，但是各自的 f1 计算出的位是不一样的，所以由此判断出 A 和 B 是不一样的数据。
  2. 举例 2：上图的 B 和 C，经过 f1 和 f2 计算出的两个位是一样的，所以由此判断出 B 和 C 是一样的数据。

小结：BF 算法虽然在一定程度上减少了 BitMap 算法中的哈希碰撞，但是终言之，只是减少而已，没法完全避免，就像上文举的案例2一样。

BF 算法优化

通过上面的图，其实很容易看出，上图中 hash function 的数量是 2，假如我们计算 3 次呢？或者 4 次甚至更多呢？诚然这可以更进一步避免数据的碰撞问题，但是太多的话却适得其反。

所以介绍优化之前我们先小结下 BF 算法的劣势，因为优化都是基于某些劣势来进行的：

  1. 误判率，或者换言之可以用 hash 碰撞的概率来帮助理解：虽然相对 BitMap 而言在一定程度上减少了 hash 碰撞的概率，但是也是存在一定的误判性的，所以对精度很高的应用场景，BF 算法并不适合。
  2. 元素的删除：因为一个位可能会对应着好几个数据，所以我们不能随意删除任意一个位上面的元素，否则其他的数据可能会判断错误。

所以，针对上面的两个点，我们逐个来突破下：

关于误判率

BF 算法优劣的影响因素，其实很容易就可以联想到，一个是根据插入的数据总量（n）来计算出最合适的位数组的大小（m）和 hash 函数的个数（k），还有一个便是最优的 误判率（使用 P(error) 表示）的选择问题。

比如：我们假设 P 为 0.01，此时最优的 m 应大概是 n 的 13 倍，而 k，应大概为 8。

详细的证明过程见下文。

关于元素删除的需求

因为数据对应的位会牵动其它的数据，所以 BF 是不可以删除位数据的，那么如果有这样的需求呢？可以使用 couting Bloom Filter 来解决，大致思路就是使用一个 counter 数组来代替位数组。

什么意思呢？简言之就是在原来的 BF 算法的位上面，不再是用简单的 0 或 1 来表示了，而是存储该位上面的数据总量，比如有两个数据经过 hash function 计算都有指向同一个位，则将该位标记为2，代表有两个数据，当删除其中一个数据时，只需要将该位上面的 2 调整为 1 即可，如此便不再影响其它数据的正确性。

应用场景

BF 算法虽然有着一定的缺点（主要是误判率），但是它的优点更为突出，所以应用场景也是很广的。

比如我们在爬虫业务下，有很多的 URL，我们可以通过 BF 算法来判断每个 URL 是否已经被我们的爬虫程序处理过。

再比如邮箱服务中垃圾邮件的过滤策略，由于垃圾邮件是海量的，我们不可能使用一个很完整的散列映射来标记每一个垃圾邮箱的地址，此处可以使用 BF 算法来标记，从而节约了容量。

另外，BF 算法在很多开源框架中也都有相应的实现，例如：

1
2
3
4
5
Elasticsearch：org.elasticsearch.common.util.BloomFilter

Guava：com.google.common.hash.BloomFilter

Hadoop：org.apache.hadoop.util.bloom.BloomFilter（基于BitSet实现）

BF 算法的数学计算过程

误判概率的证明和计算

假设布隆过滤器中的hash function满足simple uniform hashing假设：每个元素都等概率地hash到m个slot中的任何一个，与其它元素被hash到哪个slot无关。若m为bit数，则对某一特定bit位在一个元素由某特定hash function插入时没有被置位为1的概率为：

$1 - \frac 1m$

则k个hash function中没有一个对其置位的概率为：

$(1-\frac 1m)^k$

如果插入了n个元素，但都未将其置位的概率为：

$(1-\frac 1m)^{kn}$

则此位被置位的概率为：

$1-(1-\frac 1m)^{kn}$

现在考虑query阶段，若对应某个待query元素的k bits全部置位为1，则可判定其在集合中。因此将某元素误判的概率为：

$
\left(
1-\left(
1-\frac 1m
\right)^{kn}
\right)^k
$

由于 $(1+x)^{\frac1x} \sim e$，当 $x \rightarrow 0$ 时，并且 $-\frac1m$ 当m很大时趋近于0，所以：

$
\left(1-\left(1-\frac 1m \right)^{kn} \right)^k = \left(1-\left(1- \frac 1m \right)^{-m \cdot \frac {-kn}m} \right)^k \sim \left(1-e^{\frac {-nk}m}\right)^k
$

从上式中可以看出，当m增大或n减小时，都会使得误判率减小，这也符合直觉。 现在计算对于给定的m和n，k为何值时可以使得误判率最低。设误判率为k的函数为：

$f(k) = \left(1-e^{-\frac {nk}m}\right)^k$

设 $b=e^{\frac nm}$， 则简化为：$f(k)=(1-b^{-k})^k$ ，

两边取对数得：$lnf(k)=k \cdot ln(1-b^{-k})$，

两边对k求导：

$
\begin{align}
\frac1{f(k)} \cdot f’(k) &= ln(1-b^{-k}) + k\cdot \frac 1{1-b^{-k}}\cdot(-b^{-k})\cdot lnb \cdot (-1) \\
&=ln(1-b^{-k}) + k\cdot \frac {b^{-k} \cdot lnb}{1-b^{-k}}
\end{align}
$

下面求最值：

$ln(1-b^{-k}) + k \cdot \frac{b^{-k} \cdot lnb}{1-b^{-k}} = 0$
$\Rightarrow (1-b^{-k}) \cdot ln(1-b^{-k}) = -k \cdot b^{-k} \cdot lnb $
$\Rightarrow (1-b^{-k}) \cdot ln(1-b^{-k}) = b^{-k} \cdot lnb^{-k} $
$\Rightarrow 1-b^{-k} = b^{-k} $
$\Rightarrow b^{-k} = \frac12 $
$\Rightarrow e^{-\frac{kn}{m}} = \frac12 $
$\Rightarrow \frac{kn}{m} = ln2 $
$\Rightarrow k = ln2 \cdot \frac mn = 0.7 \cdot \frac mn $

因此，即当 $k = 0.7 \cdot \frac mn$ 时误判率最低，此时误判率为：

$
P(error) = (1-\frac 12)^k = 2^{-k} = 2^{-ln2 \cdot \frac mn} \approx0.6185^{\frac mn}
$

可以看出若要使得误判率 ≤1/2，则：

$
k \ge 1 \Rightarrow \frac mn \ge \frac{1}{ln2}
$

这说明了若想保持某固定误判率不变，则布隆过滤器的 位数 m 与添加的元素数 n 应该是线性同步增加的。

设计和应用布隆过滤器的方法

应用时首先要先由用户决定添加的元素数 n 和期望的误差率 P。这也是一个设计完整的布隆过滤器需要用户输入的仅有的两个参数，之后的所有参数将由系统计算，并由此建立布隆过滤器。

系统首先要计算需要的内存大小 m bits:

$
P = 2^{-ln2 \cdot \frac mn} \Rightarrow lnp = ln2 \cdot(-ln2) \cdot \frac mn \Rightarrow m = - \frac{n \cdot lnp}{(ln2)^2}
$

再由 m，n 得到 hash function 的个数：

$
k = ln2 \cdot \frac mn = 0.7 \cdot \frac mn
$

至此系统所需的参数已经备齐，接下来添加 n个元素至布隆过滤器中，再进行 query。

根据公式，当 k 最优时：

$
P(error) = 2^{-k} \Rightarrow log_2P = -k \Rightarrow k = log_2 \frac 1P \Rightarrow ln2 \frac mn = log_2 \frac 1P
$
$
\Rightarrow \frac mn = ln2 \cdot log_2 \frac 1P = 1.44 \cdot \frac 1P
$

因此可验证当 P=1% 时，存储每个元素需要 9.6 bits：

$
\frac mn = 1.44 \cdot log_2 \frac 1{0.01} = 9.6 \, bits
$

而每当想将误判率降低为原来的 1/10 ，则存储每个元素需要增加 4.8 bits：

$
\frac mn = 1.44 \cdot (log_210a - log_2a) = 1.44 \cdot log_210 = 4.8 \, bits
$

这里需要特别注意的是，9.6 bits/element 不仅包含了被置为1的 k 位，还把包含了没有被置为1的一些位数。此时的

$
k = 0.7 \cdot \frac mn = 0.7 * 9.6 = 6.72 \, bits
$

才是每个元素对应的为1的bit位数。

$k = 0.7 \cdot \frac mn$ 从而使得 P(error) 最小时，我们注意到：

$P(error) = (1-e^{-\frac{nk}{m}})^k$ 中的 $e^{-\frac{nk}{m}} = \frac 12$ ，即$(1-\frac 1m)^{kn} = \frac 12$

此概率为某 bit 位在插入 n 个元素后未被置位的概率。因此，想保持错误率低，布隆过滤器的空间使用率需为 50%。

BF 算法的代码实现

代码比较长，文章中暂不完整展示，更完整的代码 demo 详见【链接】。

下面列出了一小部分代码块，作用是根据插入的元素数量和过滤器容器的大小来计算实际的误报率：

1
2
3
4
5
6
public double getFalsePositiveProbability(double numberOfElements) {
    // (1 - e^(-k * n / m)) ^ k
    return Math.pow((1 - Math.exp(-k * (double) numberOfElements
            / (double) bitSetSize)), k);

}

image

------ 本文结束 感谢阅读 ------
0%